Mathematik

Viele Einsteine

Posted wp_blogadmin

Inhalt

Steine backen

Nach vielen Stunden Arbeit ist mein neuer 3D Drucker fertig zusammengebaut. Als eines der ersten Druckobjekte habe ich einen Sack voller „Einsteine“ gedruckt, gerade ein ganzes Kuchenblech:

Das sind Kacheln, die die Ebene lückenlos pflastern, wobei sich das Muster nie periodisch wiederholt (also nicht wie normale Bodenkacheln). Diese Kacheln in Hut- oder T-Shirt-Form heissen „Einsteine“, weil es zur Plasterung nur 1 Typ Steine braucht (ok, auch noch die umgedrehte Version). Diese Form wurde 2022 von einem Hobby-Mathematiker gefunden.

Zur Geschichte dieser Form

Die meisten (oder alle) uns geläufigen Parkettierungen sind periodisch. Man kann also eine verschobene Kopie des Musters exakt auf sich selber legen. Bei nicht-periodischen geht das nicht.

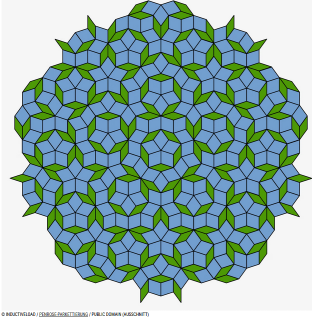
Die Einsteinkachel steht am Ende der Frage: Wie viele Kacheltypen braucht man mindestens, damit zwingend eine nichtperiodische Parkettierung entstehen muss? Im Verlaufe der Zeit kam man von 20426 (1966) bis zu 2 Kacheln herunter (Penrose 1974). Dies ist die Penrose-Kachelung:

Muster mit Einsteinen

Mit den Steinen (in mehreren Farben) lassen sich auch viele interessante Muster legen. Der Stein ist erstaunlich „anlegefreudig“…

Nichtperiodisches Belegen der Ebene

Das  ist ziemlich schwierig, da sich das Muster nie wiederholt. Man kann also nie ein Stück nach einem gleichbleibenden Muster hinlegen. Konkret heisst das: man beginnt und landet irgendwann in einer Sackgasse, wo man nicht weiterkommt und Steine wegnehmen muss. Nur: welche sind denn falsch?! Es ist nicht klar, welche man wegnehmen muss.

Aber es gibt ein Verfahren: aus einfacherer Kacheln lassen sich immer grössere, im Prizip ähnliche (aber nicht ganz identisch geformte) „Superkacheln“ legen. Aus diesen macht man noch grössere Superkacheln usw.  Es gibt 4 Typen (linke Seite des Blattes):

  • Der 1. Typ (links oben) besteht aus 1 Einstein-Kachel  (2. Dreiecksrahmen links; bei mir rot), die von 3 Steinen (orange bei mir) so umgeben wird, dass man eine 6-eckige Form hat.
  • Aus je 2 Steinen macht man den 3. resp. 4 Typ.
  • Nimmt man 3 Typ 1-Superkacheln um einen zentalen Einstein (bei mir grün) und ergänzt sie mit je 3 länglichen Typ 3/4-Superkacheln (links unten, bei mir rot und grün) so entsteht die „Supersuperkachel“ rechts oben mit schon 25 Steinen.
  • Dieser wird dann ähnlich vergrössert (mach schaue die Figur rechts unten auf dem Blatt an)

Prinzipiell kann man so weitermachen. Aber ganz stupid regelmässig wird es eben nie (es gibt Regeln, was man wo anlegen muss) – was die Schwierigkeit des Puzzles eben ausmacht.

Zum Lesen