Wir nennen das Gefäss mit 8 Liter Inhalt A, das mit 5 heisse B und das dritte mit 3 Liter sei C. Den Füllstand können mir vereinfacht mit einer 3-stelligen Zahl kodieren, z.B. bedeute 800 = 8 Liter im Gefäss A, 0 Liter in B und 0 in C.
Die Lösung lautet in dieser Notation: 800 → 350 → 323 → 620 → 602 → 152 → 143.
Man kann solche Rätsel systematisch lösen, wenn man bemerkt, dass die Summe (die gesamte Flüssigkeitsmenge) aller Zahlen konstant ist. Man kann einen Füllstand abc mit der Bedingung a+b+c = 8 als Punkt eines Dreiecks auffassen – vielleicht erinnert man sich noch an die Schwerpunktskoordinaten (baryzentrische Koordinaten) aus der Physik? Im Dreieck ist 800 oben (Ecke A), 080 links unten (Ecke B), 008 rechts unten (Ecke C). Jeder Füllstand entspricht einem Punkt im Dreieck.
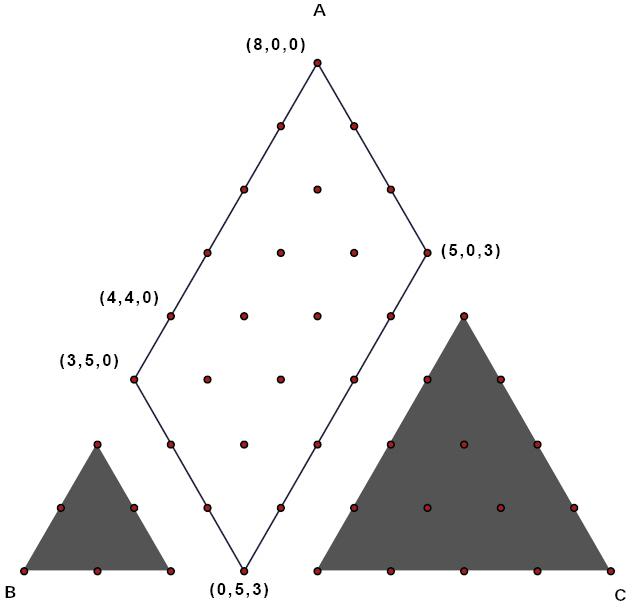
Durch Umschütten bewegt man sich in diesem Dreieck nach folgenden Regeln:
- Start ist der Punkt 800 oben (alle 8 Liter im Gefäss A)
- man bleibt auf dem Gitterraster, da die Mengen immer ganze Liter und keine Bruchteile von Litern sind
- man bleibt im umrandeten Parallelogramm, die Eckpunkte sind 800, 350, 503, 053. Dann sind 1 oder 2 Gefässe ganz leer oder voll. Punkte ausserhalb können nicht erreicht werden.
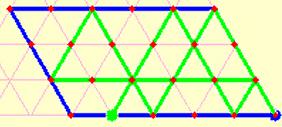
- Immer wenn man ein Gefäss ganz leert oder füllt, „läuft“ man auf den Rand zu und landet schliesslich auf dem Rand.
- vielleicht am schwierigsten einzusehen ist die letzte Regel: wenn man wieder vom Rand „wegläuft“, indem das Wasser umgiesst, gilt Einfallswinkel = Ausfallswinkel, d.h. man bewegt sich wie eine Billardkugel!
Damit stehen wir einfach vor der Aufgabe, durch Billardspielen im Parallelogramm einen Punkt auf dem Rand mit 4 Litern zu treffen! Mögliche Punkte sind nur 440, 413, 143.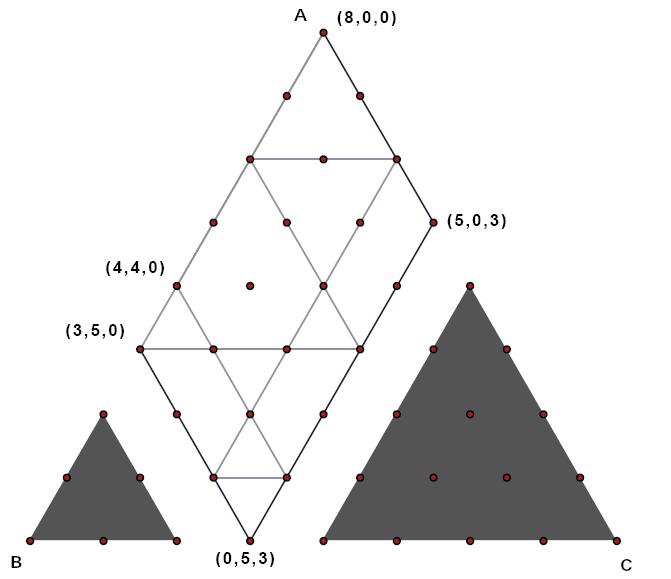
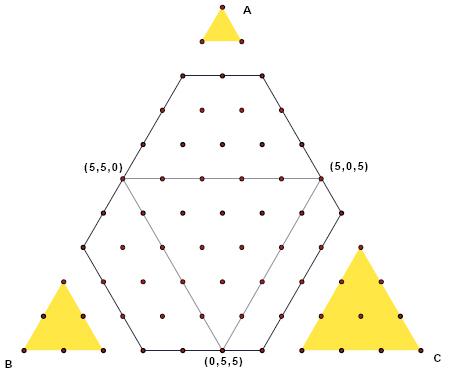
Zur Zusatzfrage: Können wir mit 3 Gefässen mit 8, 7, 6 Liter Inhalt auch 5 Liter abmessen? Dies ist nicht lösbar, man versuche es! Grafisch etwas einfacher ist die Aufgabe, mit 8,7,6 Liter und 10 Liter Wasser 5 abzumessen: mit den obigen Überlegungen stellt man fest, dass alle Lösungen auf einem geschlossenen gleichseitigen Dreieck mit den Ecken 550, 055, 505 liegen. In dieses Dreieck kommt man nur hinein, wenn man schon darauf startet (Billardbedingung!).
Link: http://www.cut-the-knot.org/ctk/Water.shtml (mit Java-Demo)
Neue kleine Quizfrage
Wie kann man die Zahlen 23 und 27 mit der Zahl 1, Additionen (+), Multiplikationen (x) und Klammern möglichst kurz schreiben? Wie oft wird die Zahl 1 gebraucht ?
Beispiele:
5 = (1+1)×(1+1)+1
13 = (1+1+1)×(1+1)×(1+1)+1