Für diese Quizfrage habe ich keine genaue Lösung erwartet und auch meine Lösung soll ohne die vollständigen Formeln auskommen – vielmehr möchte ich einige Bemerkungen anbringen, die unter anderem das Verständnis des Smith-Diagramms erleichtern.
Vereinfachungen: wir nehmen an, dass der Punkt A der Nullpunkt O in der xy-Ebene sei. Die Punkte B und C sollen einen Abstand <1 von O haben (mit einer willkürlichen Längeneinheit). Die Strahlungsintensität sei gleich 1/r2. Strahlendosis = Strahlenintensität mal Weglänge (wir gehen immer mit Geschwindigkeit 1).
Kurzversion: der Weg mit der kleinsten Strahlendosis ist ein Kreisbogen. Der Kreis ist durch die Punkte A (Strahlungsquelle), B (Start) und C (Ende) bestimmt.
Begründung: Wir haben den kürzesten Weg zwischen B und C zu bestimmen, haben aber eine ungewohnte Art Längenmessung: ein Wegstück im Abstand r von wird mit 1/r2, der Strahlenintensität, gewichtet. Um die Länge wie gewohnt messen zu können, müssen wir eine geometrische „Verzerrung“ durchführen, die alle Längen mit eben diesen 1/r2 verzerren. Eine solche Verzerrung erfolgt durch die Inversion am Kreis (Spiegelung am Kreis): ein Punkt P im Abstand |OP| = r wird zu einem Punkt P‘ mit Abstand |OP’| = 1/r abgebildet. Es gilt also |OP| / |OP’| = r2. Beide Punkte liegen auf dem gleichen Strahl (d.h. Winkel bleibt gleich).
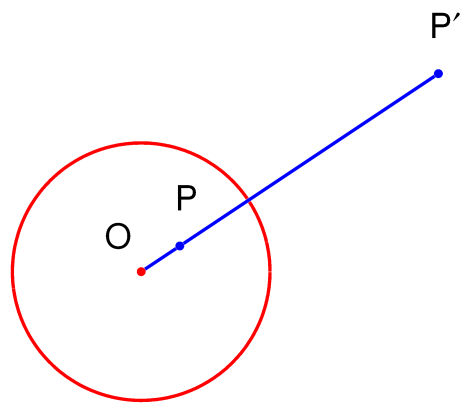
Inversion am Kreis: |OP| = r, |OP’| = 1/r
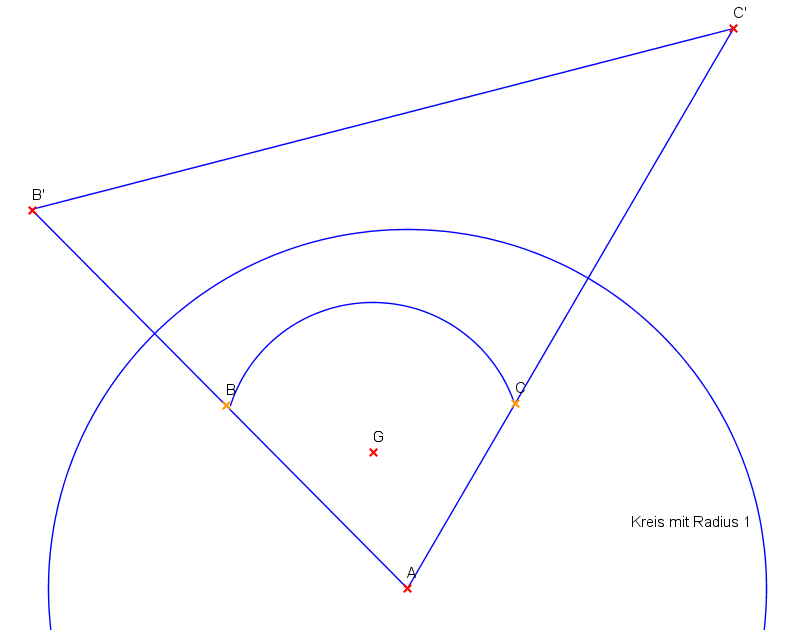
Lösung: Kreisbogen durch ABC
Der Gedankengang zur Lösung ist wie folgt: Wir bilden die Punkte B und C mit der Inversion auf B‘ und C‘ ab. Wir nehmen die noch unbekannte Lösungskurve zwischen B und C und zerteilen sie in viele kurze Wegstücke. Ein solches Wegstück W beginne beim Punkt P und habe die Länge s. Die Strahlenintensität ist 1/|OP|2. Die Dosis ist also gleich s/|OP|2. Das Wegstück wird durch die Inversion zu einem Wegstück W‘ mit Länge s/|OP|2 beim Punkt P‘ abgebildet. Die Strahlendosis ist also gleich der Weglänge von W‘. Wir setzen alle Wegstücke zusammen und erhalten: die Strahlendosis auf dem unbekannten Weg von B nach C ist gleich der Länge des invertierten Wegs von B‘ nach C‘. Die Dosis ist also minimal, wenn der invertierte Weg kürzestmöglich ist. Der kürzeste Weg zwischen B‘ und C‘ ist aber eine Gerade! Wir nehmen also die Strecke B’C‘ und invertieren sie zurück. Wir verwenden dabei, dass die Inversion Kreise auf Kreise abbildet (Geraden zählen als Spezialfälle von Kreisen).
Was es noch zu sagen gäbe:
1) Wir haben eine ungewohnte Längenmessung vorgefunden und daraus ungewohnte „kürzeste Geraden“ bestimmt. In der Allgemeinen Relativitätstheorie bekommen solche Fragen physikalische Bedeutung, indem die Längenmessung mit der Massenverteilung und der Krümmung des Raumes verbunden wird. Die Bestimmung kürzester Wege (Geodäten genannt) ist meist sehr schwer oder unmöglich. Auf der Erdoberfläche sind die Geodäten Grosskreise.
2) Das schwierige Problem haben wir durch eine geometrische Transformationen – einen Wechsel des Standpunktes – in ein einfacheres umgewandelt.
3) die Inversion am Kreis ist wie erwähnt kreistreu und auch winkeltreu. Dies sind an und für sich schon hübsche Aufgaben für die Leser…
4) Was hat dies mit der Smith Chart zu tun? Eine ausführliche Diskussion würde hier zu weit führen; ich habe einen solchen Artikel für ein späteres QUA vorgesehen. Als Appetitmacher nur die Behauptung, dass sich die rechte Halbebene der komplexen Gauss’schen Zahlenebene kreistreu und winkeltreu auf das Innere des Einheitskreises abbilden lässt. Die Abbildung ist sehr ähnlich zur Inversion am Kreis.
Wem diese Begriffe nichts sagen, widme ich gerne den erwähnten Artikel…
Abbildung der rechten Halbebene r>0 auf das Innere des Einheitskreis, das Smith-Diagram. Geraden gehen in Geraden oder Kreise über, die rechten Winkel bleiben erhalten.
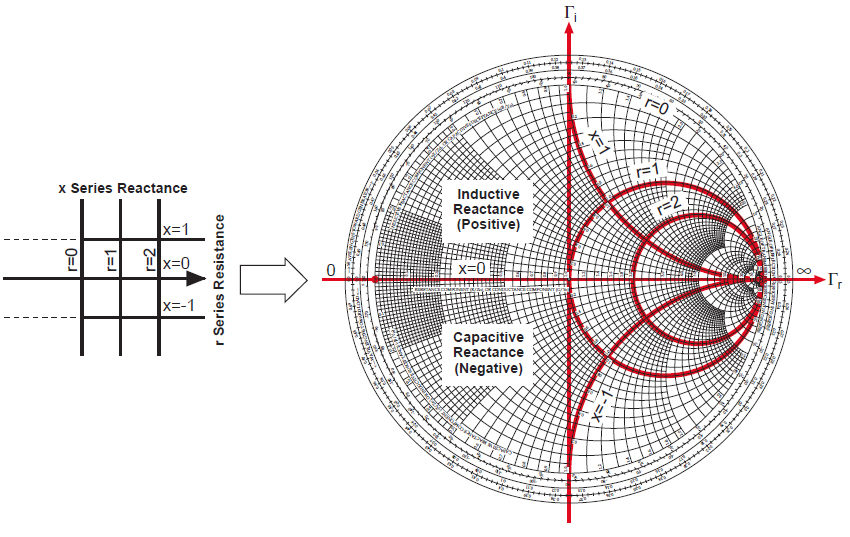
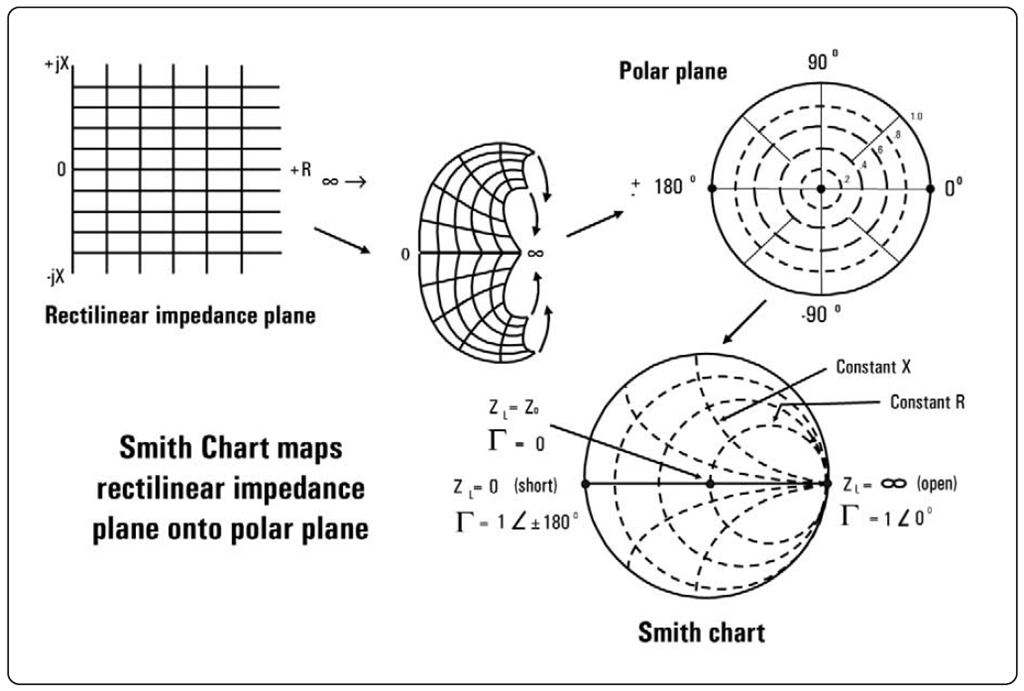
Quelle: Agilent
Die Vorteile des Smith Diagramms liegen darin, dass wir den Standpunkt wechseln können, wie er unseren Berechnungen besser angepasst ist. Dass dabei Kreise in Kreise (oder Geraden) abgebildet werden, muss so sein und machen die Konstruktionen im Diagramm erst möglich. Praktisch ist auch, dass das Kreisdiagramm handlicher ist als eine unendlich grosse Fläche.
Nicht nur das Innere der Einheitskreisscheibe lässz sich winkeltreu (genauer gesagt: konform) auf die rechte Halbebene abbilden. Noch viel mehr als das ist möglich, wie ein Video auf Youtube erklärt:

Neue Quizfrage
Es gibt die Anekdote, dass Euler von der russischen Zarin Katharina der Grossen folgende Aufgabe erhalten hat:
Beim Divisionsball ordnet jedes der sechs anwesenden Regimenter für jeden der sechs Dienstgrade je einen Offizier ab: Die sechsunddreissig Offiziere sollten zur Feier des Tages so im Quadrat aufgestellt werden, dass in jeder Zeile und jeder Spalte genau ein Offizier jeden Regiments und jeden Dienstgrades steht.
Man löse diese Aufgabe für 3 Regimenter. Das ist noch einfach…
Sie wird etwas übersichtlicher, wenn man anstatt Offiziersränge und Regimenter Farben verwendet: man nehme 3 Farben, 9 Kartonquadrate und zeichne auf ein Blatt Papier ein grosses Quadrat mit 3×3=9 Feldern. Jedes Kartonquadrat wird mit einer Farbe eingefärbt und erhält zusätzlich einen Farbfleck in die Mitte gesetzt (total 3×3 = 9 verschiedene Farbkombinationen). Man lege die 9 farbigen Kartonquadrate auf die 9 Felder des gezeichneten Quadrates wie beschrieben (die Farbe des Kartonquadrat symbolisiert das Regiment, der Farbfleck den Dienstgrad).
Update 20170812