Jost Bürgi – das unbekannte Genie

Tycho Brahe und Johannes Kepler sind uns allen ein Begriff, aber den Jost  Bürgi kennen die meisten von uns (noch) nicht. Der Toggenburger Uhrmacher und Mathematiker war seiner Zeit voraus und verdient meiner Meinung nach zu recht den Titel eines Genies. Man kann sich mit dem prächtig illustrierten Buch [1] ja selber ein Bild machen.

Neben seinen Uhren und Messinstrumenten wurde er schon vor einiger Zeit als einer der Erfinder der Logarithmen erkannt. Meist werden diese John Napier zugeschrieben; das erwähnte Buch geht ausführlich auf diese Geschichte ein.

Ich möchte mich dagegen mit seiner Berechnung von Tabellenwerken mit Sinuswerten beschäftigen. Jost Bürgi hatte ein Rechenverfahren erfunden, das als „Kunstweg“ anscheinend nur speziell eingeweihten Personen bekannt war. Erst im Jahr 2013 wurde ein Manuskript entdeckt, das die Methode erklärt [1], [3-6].

Ein genialer Kunstweg

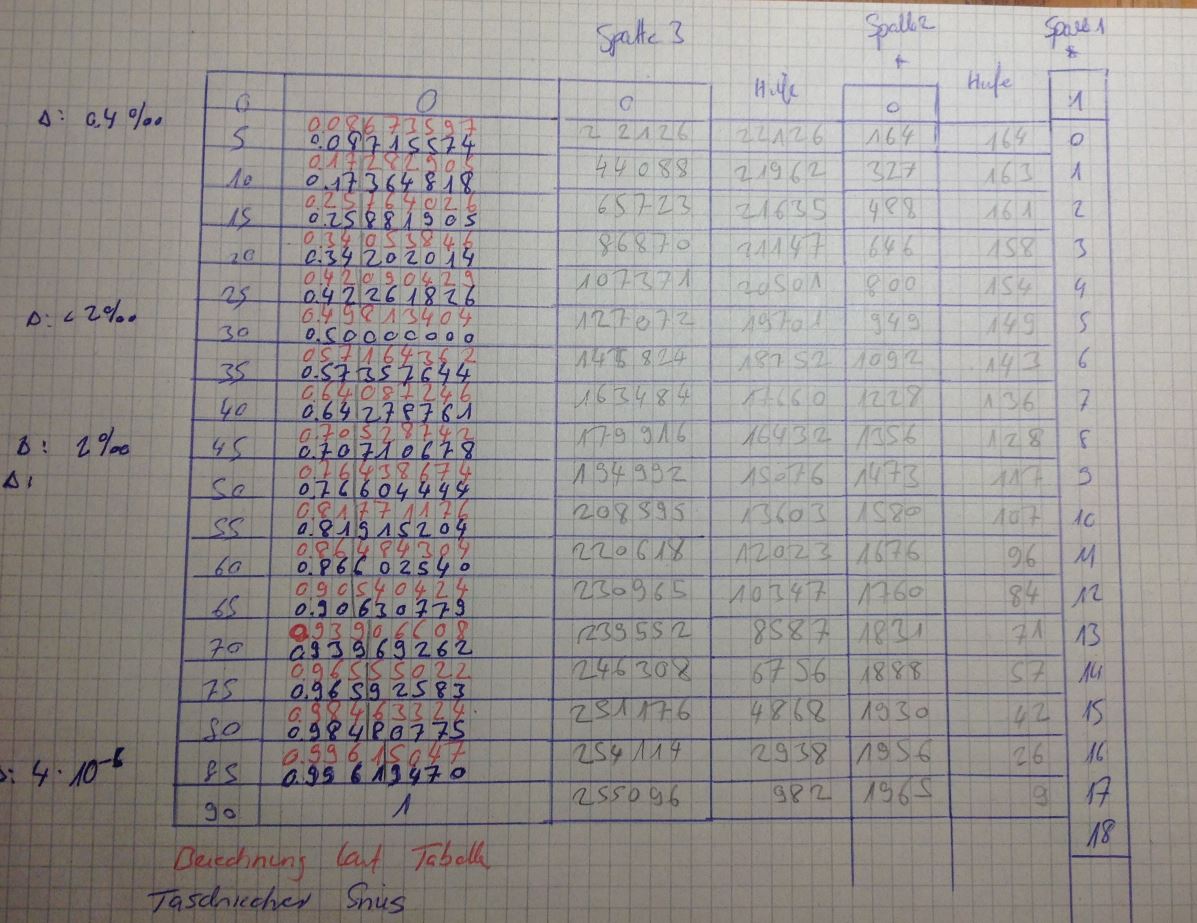
Das Verfahren berechnet iterativ eine Tabelle von Sinuswerten zu aequidistanten Werten, ausgehend von einer groben Näherung. Im Original ist ein Beispiel für eine Tabelle mit 10-Grad Schritten zu sehen. Es werden nur ganzzahlige Rechnungen durchgeführt bis zum allerletzten Schritt der Division. Das Verfahren wird in einer speziellen Tabellenform schlangenförmig fortschreitend von rechts unten durchgeführt.

• in Spalte 1 rechs wird eine grobe Näherung eingetragen: 0 bis 12. Dabei entspricht 12 dem Winkel 90 Grad.
• 12 wird halbiert zu 6
• Zu 6 wird die 11 rechts oberhalb addiert und dies weitergeführt, bis man oben bei der 0 anlangt: 6+11=17,17+10=27, 27+9=36…
• die Additionen werden gleichermassen von oben nach unten durchgeführt (ohne Halbierung der obersten Zahl)
• die unterste Zahl 62 wird halbiert zu 31 und das Verfahren wiederholt.
• im letzten Schritt wird durch Division durch die grösste Zahl normiert, sodass sin(90°) = 1.

Im Mittelalter war es üblich, im Sexagesimalsystem zu rechnen (60er System). Deshalb steht in der Tabelle 0.57+4 = 1 1, dies ist dezimal 61.

Die mathematische Erklärung der Konvergenz findet man in [4].

Wie man darauf kommt, ist mirakulös. Ein Erklärungsversuch: Das Verfahren kehrt gewissermassen die Berechnungsmethode der zweiten Differenzen um (siehe [3,4]). Diese zweiten Differenzen kennt man aus den arithmetischen Reihen höherer Ordnung, z. B. sind die zweiten Differenzen einer Polynomfunktion zweiten Grades konstant. Bei der Sinusfunktion sind diese ein konstantes (negatives) Vielfaches des Funktionswertes an derselben Stelle (die zweite Ableitung ). Jost Bürgi kannte diese Rechenverfahren sicher gut, da sie allgemein üblich in astronomischen Berechnungen waren.

Allerdings meinen ein paar Stimmen [5], das seine grösste Sinus-Tabelle nicht nur alleine mit dieser Methode, sondern auch mit herkömmlicher Interpolation verfeinert wurde. Das tut der ganzen Sache keinen Abbruch, da die Tabelle für alle Gradwerte von 1° bis 90° damit erstellt worden ist.

Von Hand

Das Verfahren von Bürgi ist das einzige, das ich auswendig im Kopf behalten kann. Es ist so einfach und dabei sehr genau mit wenig Rechenaufwand. Ein Nachteil ist nur, dass immer eine ganze Tabelle berechnet wird, keine einzelnen Werte.

 

Mit Excel

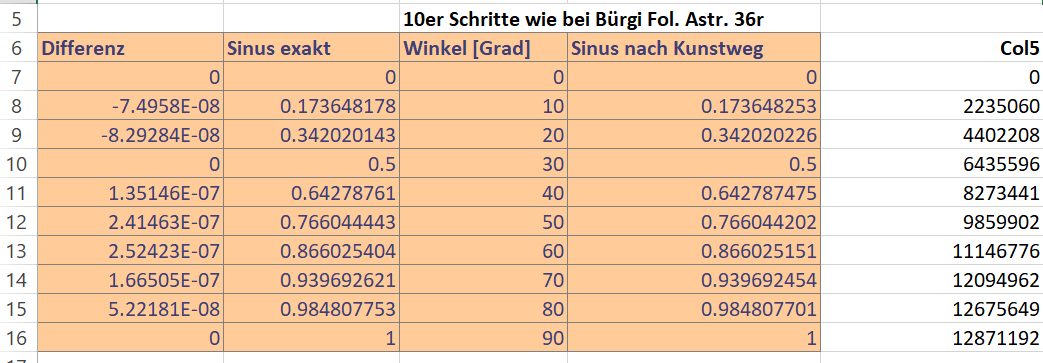
Die Berechnungen lassen sich mit kleinem Aufwand in Excel realisieren. Mit 5 Spalten erhält man schon ein Genauigkeit von 10^-7 oder besser.

 

Quellen zur Sinusberechnung

1. Fritz Staudacher: Jost Bürgi, Kepler und der Kaiser. Neue Zürcher Zeitung NZZ Libro; Auflage: 3 (16. Dezember 2015), ISBN 978-3038101383.
2. NZZ Ein Kunstweg zur Berechnung von Sinuswerten
3. Jürg Waldvogel, Vortrag Swiss Physical Society SPS, Annual Meeting 2016, 08/23-25
4. Menso Folkerts, Dieter Launert, Andreas Thom Jost Bürgi’s Method for Calculating Sines. arXiv:1510.03180v2
5. Peter Ullrich: The mathematics behind Jost Bürgi’s method for calculating sine tables. PAMM · Proc. Appl. Math. Mech. 16, 891 – 892 (2016), http://onlinelibrary.wiley.com/doi/10.1002/pamm.201610434/pdf
6. Grégoire Nicollier: How Jost Bürgi Computed the Sines of All Integer Angles in 1586, https://www.cut-the-knot.org/blue/JostBurgi.shtml

Weitere Quellen zur Logarithmusberechnung

1. Ein Gymi-Lehrstück
2. weiteres didaktisches Material