Inhalt
Python/Jython in der Schule
Für mein erstes Praktikum auf meinem Weg zum Lehrer habe ich einer Schulklasse (Gymnasium, Tertia) ein paar Stunden Informatikunterricht erteilt. Als Thema wählten wir einige Kapitel aus dem „Lehrbuch“ Tigerjython aus. Dieses besteht aus einem mehrere 100 Seiten dicken online Buch und einer dazugehörigen Programmierumgebung für Python. Programmiert wird also in Python, die Umgebung und einige Zusatzmdoule sind in Java realisiert. Bestechend ist für mich daran, dass keine Installationen nötig sind (Kopieren reicht, z.B. auch auf einen USB Stick) und fast alle Programme aus dem Buch per Copy&Paste lauffähig sind.
Ich habe Unterlagen für 5 Doppellektionen erstellt und hier im Blog verlinkt.
Kryptographie (Tigerjython Kap. 10.5)
- Präsentation Kryptologie
- Aufgabenblatt mit Zusatzaufgaben
- Lösung Caesar Histogramm
- Lösung Skytale Verschlüsselung und Entschlüsselung
Die Berechungen zum RSA-Verfahren füge ich hier exemplarisch direkt ein. Die Zahlentheorie dahinter ist nicht so banal, wenn man sie lückenlos präsentieren will.
Die Berechnungen der Modular Inversen erfolgt im Buch mit einem Brute Force Verfahren (man rechnet einfach alle durch). Berechnen kann man sie mit dem Satz von Euler resp. mit dem erweiterten Euklidischen Algorithmus.
# RSA Berechungen # RSA Wiki # Beispiel: (-1071)*11 + 2 * 5891 = 1 # Rechnungen im Tigerjython from math import * p = 73 q = 151 m = p * q phi = (p-1) * (q-1) e = 11 d = e** (phi - 1) % phi print "p =", p print "q =", q print "m =", m print "phi =", phi print "e =", e print "d = e** (phi - 1) % phi = ", d print "d*e = ", d * e print "d*e mod phi =", d*e, "modulo", phi,"=", d * e % phi
Berechnung der modular Inversen mit dem erweiterten Euklidischen Algorithmus (wie er im Beweis des Lemma von Bézouts gebraucht wird):
# RSA Berechungen
# RSA Wiki
# Bezout Rechner: http://www.dcode.fr/bezout-identity
# (-1071)*11 + 2 * 5891 = 1
# RSA Caclculator https://www.cs.drexel.edu/~jpopyack/IntroCS/HW/RSAWorksheet.html
# https://de.wikibooks.org/wiki/Algorithmensammlung:_Zahlentheorie:_Euklidischer_Algorithmus
# https://de.wikipedia.org/wiki/Erweiterter_euklidischer_Algorithmus
# Berechung mit Lemma von Bezout
# http://www.inf-schule.de/kommunikation/kryptologie/rsa/modmultiplikation/station_berechnungmodinv
# siehe auch https://www.cryptool.org/de/
def erweiterterEuklidischerAlgorithmus(a, b):
aalt = a
amitte = b
xalt = 1
xmitte = 0
yalt = 0
ymitte = 1
while amitte != 0:
q = aalt // amitte
aneu = aalt - q * amitte
xneu = xalt - xmitte * q
yneu = yalt - ymitte * q
xalt = xmitte
xmitte = xneu
yalt = ymitte
ymitte = yneu
aalt = amitte
amitte = aneu
print(amitte, ' = ', xmitte, ' * ', a, ' + ', ymitte, ' * ', b)
return (aalt, xalt, yalt)
def modInv(a, m):
(ggt, x, y) = erweiterterEuklidischerAlgorithmus(a, m)
if ggt > 1:
return -1
else:
if x < 0:
x = x + m
return x
erweiterterEuklidischerAlgorithmus(11, 11023)
print modInv(11,10800)
Endliche Automaten
Die Lösung der Aufgabe „Fleissiger Biber“ sei auch hier direkt abgedruckt. Zur sehr interessanten Theorie dahinter siehe Wikipedia. Der Automatengraph sieht dermassen aus:
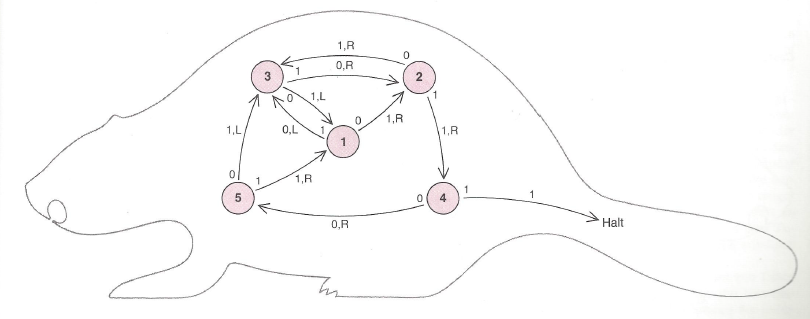
# Busy beaver mit 3 Zuständen
# schreibt in 13 Schritten 6 Einer auf ein leeres Band
# A. Bieri
from gconsole import *
tape = range(2 * 10)
for i in range(2 * 10):
tape[i] = "0"
tape_middle = 10
tape_pos = 0 #-9 bis 9, es wird dazu tape_middle addiert
State = enum("state_1", "state_2", "state_3", "state_halt")
state = State.state_1
Events = enum("read0", "read1")
def getField():
if tape[tape_middle + tape_pos] == "0":
ch = Events.read0
elif tape[tape_middle + tape_pos] == "1":
ch = Events.read1
return ch
makeConsole()
while state != State.state_halt:
gprintln("State: " + str(state))
event = getField()
if event == Events.read0:
if state == State.state_1:
state = State.state_2
tape[tape_pos + tape_middle] = "1"
tape_pos = tape_pos + 1
elif state == State.state_2:
state = State.state_1
tape[tape_pos + tape_middle] = "1"
tape_pos = tape_pos - 1
elif state == State.state_3:
state = State.state_2
tape[tape_pos + tape_middle] = "1"
tape_pos = tape_pos - 1
if event == Events.read1:
if state == State.state_1:
state = State.state_3
tape[tape_pos + tape_middle] = "1"
tape_pos = tape_pos - 1
elif state == State.state_2:
state = State.state_2
tape[tape_pos + tape_middle] = "1"
tape_pos = tape_pos + 1
elif state == State.state_3:
state = State.state_halt
tape[tape_pos + tape_middle] = "1"
gprintln("State: " + str(state))
gprintln(tape)
SQL Teil 1
- Präsentation I und Aufgabenblatt I
- Lösung Palindrom Aufgabe mit Wortliste
- CSV Listen personen schule
- Aufgabe2d-Lösung.py
- Aufgabe3a-Lösung.py
- Aufgabe3b-Lösung.py
- Aufgabe3c-Lösung1.py Aufgabe3c-Lösung2.py Aufgabe3c-Lösung3.py
- create-unidb.py
- CSV-Adressen-Lösung.py
- Hausaufgabe: average-db.py select-bern.py
Auch hier ein Beispiel zur Veranschaulichung:
import csv #zum Lesen von CSV Dateien
with open('example3.csv') as csvfile:
readCSV = csv.reader(csvfile, delimiter=';') #Felder durch Strichpunkt getrennt
lNamen = []
lVornamen = []
lWohnort = []
lGeschlecht = []
lAlter = []
for row in readCSV:
print("Ganze Zeile: ", row)
lNamen.append(row[0])
lVornamen.append(row[1])
lWohnort.append(row[2])
lGeschlecht.append(row[3])
lAlter.append(row[4])
print("Liste Namen: ")
print (lNamen)
print("Liste Vornamen: ")
print (lVornamen)
print("Liste Wohnorte: ")
print(lWohnort)
print("Liste Geschlechter: ")
print(lGeschlecht)
print("Liste Alter: ")
print(lAlter)
print("Altersdurchschnitt")
# hier Code einfügen
dschnitt = 0
for i in lAlter[1::]:
dschnitt += int(i)
print(dschnitt/(len(lAlter)-1))
SQL Teil 2
- Präsentation SQL 2 und Aufgabenblatt SQL2
- Aufgabe1a-Lösung.py Aufgabe1b-Lösung.py
- Aufgabe 2
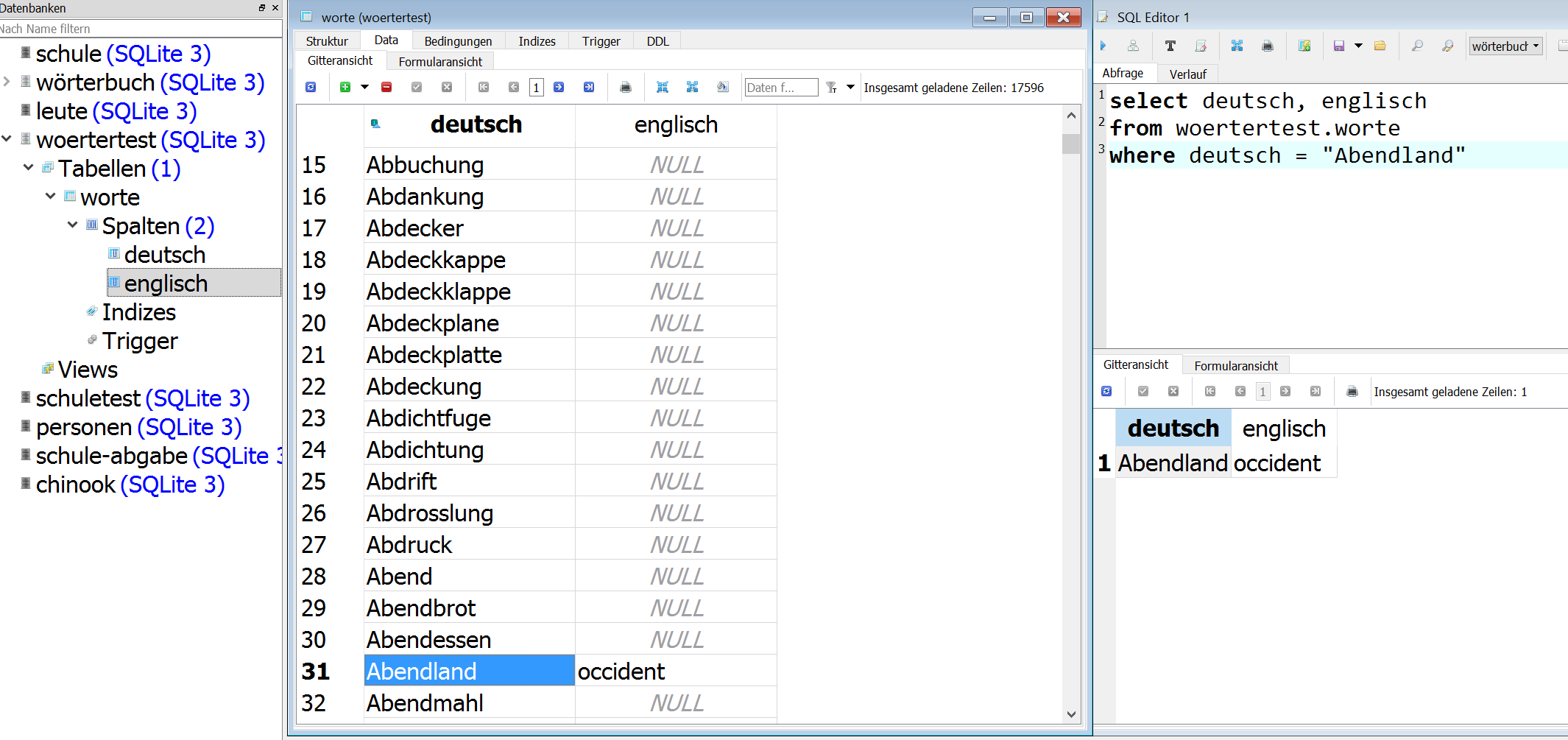
- Aufgabe2d-Lösung.sql
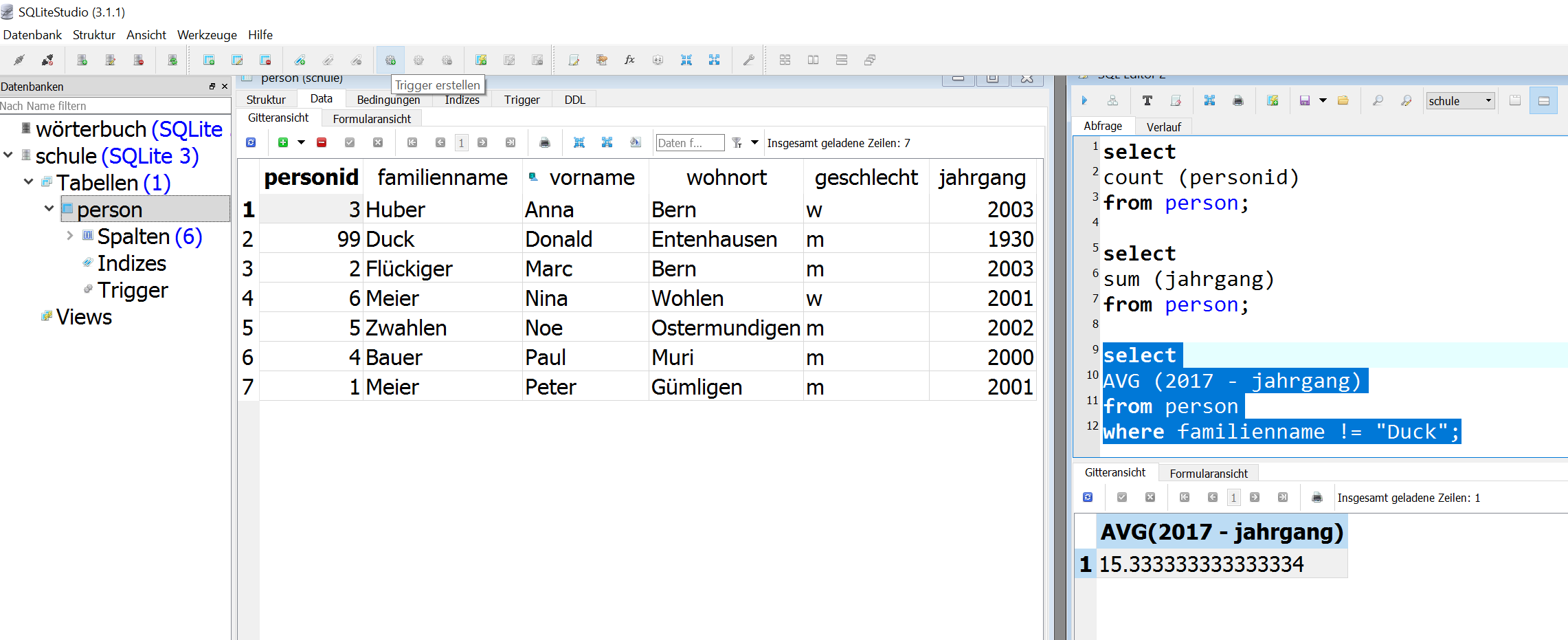
- Aufgabe 3a im SQLite Studio
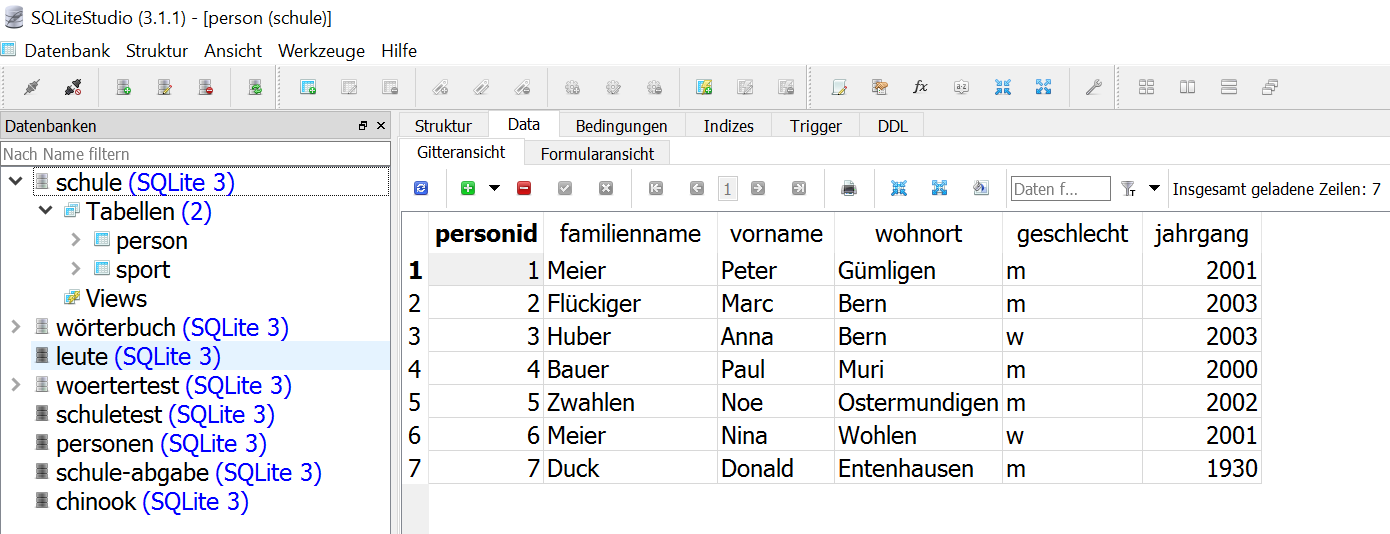
- Aufgabe 3b
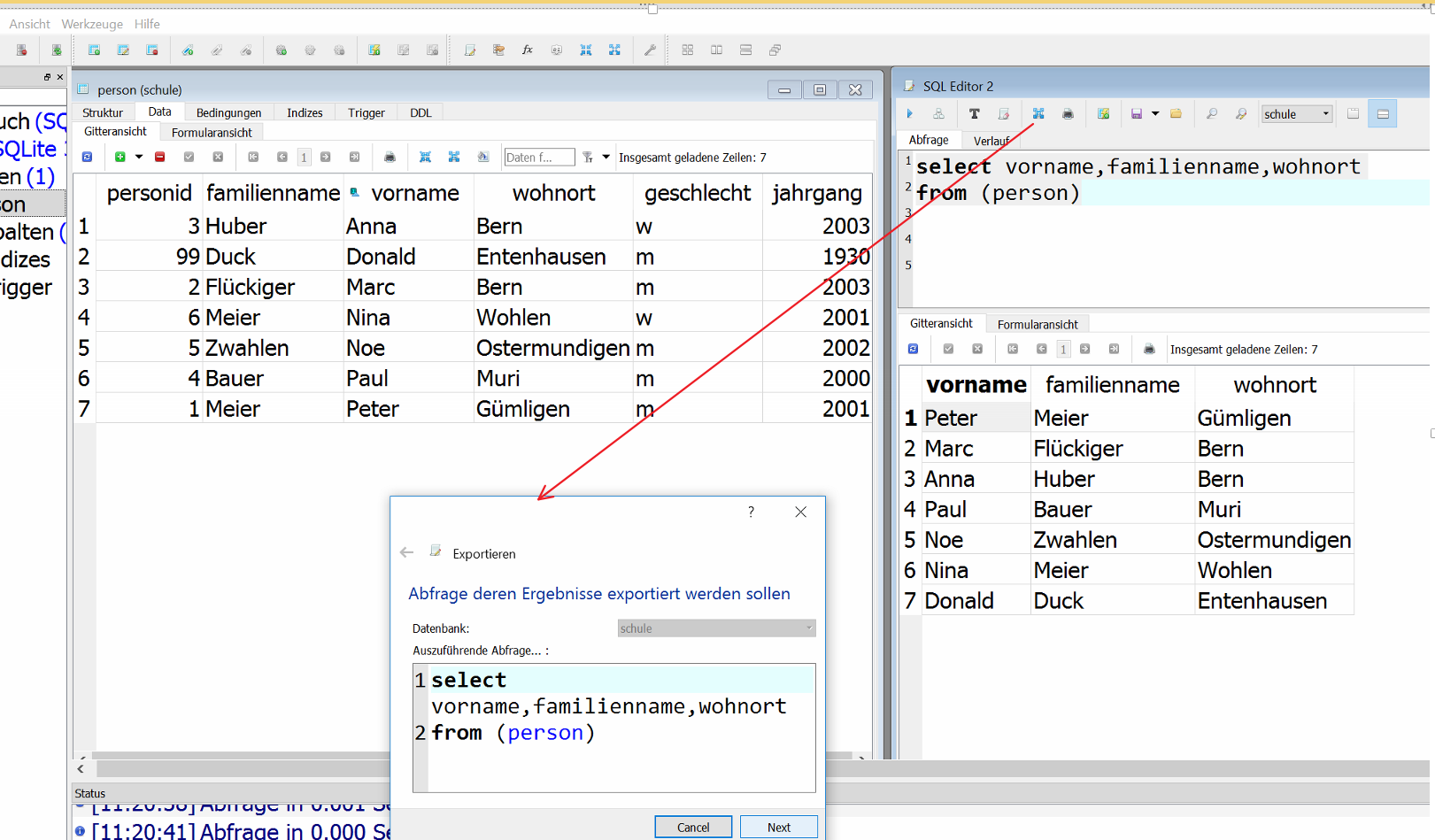
- Aufgabe 3c-d
Spektralanalyse
- Präsentation Fourier – V3, mit separatem Audio (Fledermäuse) und Video (LoRa)
- Aufgabenblatt und die Audio Dateien dazu
- Gezeiten – WhyDoMath
Zeit- und Spektralanalyse für einige Grundfunktionen wie Rechteck- und Dreieckfunktionen:
from gpanel import *
from soundsystem import *
fs = 40000 # Sampling frequency
A = 1000 # Amplitude
samples = [0] * 120000 # sampled data for 3 s
t = 0
dt = 1 / fs # sampling period
makeGPanel(0, len(samples), -33000, 33000)
for i in range(120000):
samples[i] = sine(A, 400, t) + sine(A, 390, t)
#samples[i] = sine(A, 4000, t) + sine(A/2, 3000, t)
#samples[i] = sine(A, 500, t)
#samples[i] = square(A, 1000, t)
#samples[i] = triangle(A, 1000, t)
#samples[i] = sawtooth(A, 1000, t)
#samples[i] = chirp(A, 1000, t)
#samples[i] = sine(100, 4000, t) * sine(100, 3000, t)
t += dt
openMonoPlayer(samples, 40000)
play()
for i in range (len(samples)//100):
draw(100*i, 10*samples[i])
# Kurvenform anzeigen:
# experimentiere mit der Anzahl der Punkte und der y-Achse
# "Mikroskop":
#for i in range (len(samples)//100):
# draw(100*i, samples[i])
# Gesamtsicht:
#for i in range(12000):
# draw(i, samples[i])
# mit Faktor 10 vergrössert:
#for i in range(120000):
# draw(i, 10*samples[i])
from gpanel import *
from soundsystem import *
def showSpectrum(text):
makeGPanel(-2000, 22000, -0.2, 1.2)
drawGrid(0, 20000, 0, 1.0, 10, 5, "blue")
title(text)
lineWidth(2)
r = fs / n # Resolution
f = 0
for i in range(n // 2):
line(f, 0, f, a[i])
f += r
n = 10000
fs = 40000 # Sampling frequency
A = 1000 # Amplitude
samples= [0] * 120000 # sampled data for 3 s
t = 0
dt = 1 / fs # sampling period
for i in range(120000):
#samples[i] = sine(A, 4000, t) + sine(A/2, 3990, t)
#samples[i] = sine(A, 4000, t) + sine(A/2, 3000, t)
#samples[i] = sine(A, 500, t)
samples[i] = square(A, 1000, t)
#samples[i] = triangle(A, 1000, t)
#samples[i] = sawtooth(A, 1000, t)
#samples[i] = chirp(A, 1000, t)
#samples[i] = sine(100, 4000, t) * sine(100, 3000, t)
t += dt
openMonoPlayer(samples, 40000)
play()
a = fft(samples, n)
showSpectrum("Spectrum")
Update 20171117: SQL Skript und Python Skript von Uwe Ziegenhagen. Update 20180114 typos